FC97The Birth of Modern Science

Western science, like so many other aspects of Western Civilization, was born with the ancient Greeks. They were the first to explain the world in terms of natural laws rather than myths about gods and heroes. They also passed on the idea of the value of math and experiment in science, although they usually thought only in terms of one to the exclusion of the other. It is easy for us to be critical of their early scientific theories, but we must remember several things about their world. First, by that time, the human race had learned to exploit the environment for survival (e.g., agriculture, woven cloth, metallurgy, etc.), but knew little about the physical laws that rule nature and the universe. Also, there were no telescopes, microscopes, or other instruments to aid the naked eye in its observations and measurements. Everything they learned about the natural world had to be done with the unaided senses and whatever rational deductions they could make based on them.

Knowing the limitations the Greeks operated under helps us appreciate the scientific view of the world they evolved and handed down to posterity. The Greeks realized the limitations to their observations, and many of them argued that relying on one's senses was a faulty way to unravel the mysteries of the universe. The philosopher, Plato, compared our perception of reality to that of a man chained to the wall of a cave who only sees shadows from the outside world cast against the opposite wall.

However, other Greek philosophers argued that use of the senses for observation, as faulty as it may be, was still worthwhile. One of these Greeks, and by far the most influential figure in Western science until the 1600's, was the philosopher, Aristotle, who created a body of scientific theory that towered like a colossus over Western Civilization for some 2000 years. Given the limitations under which the Greeks were working compared to now, Aristotle's theories made sense when taken in a logical order.

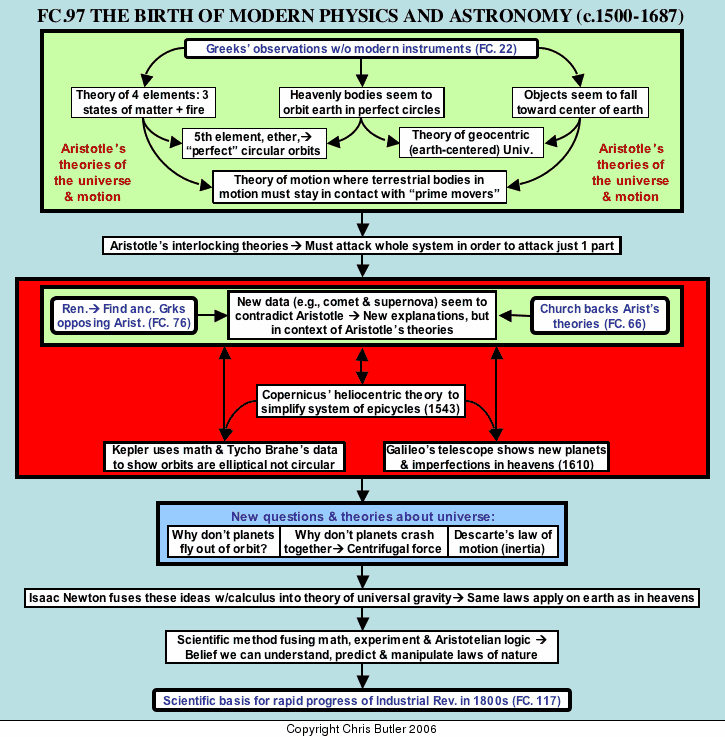
Three basic observations laid the foundations for Aristotle's view of the universe and laws of motion: First of all, there was the theory of the elements. The Greeks came up with several theories on the elements, including Democritus' atomic theory, the idea that all matter is composed of tiny indivisible particles called atoms (from the Greek atomon = indivisible). Other Greeks observed three basic states of matter: solid, liquid, and gas. As a result, they came up with four basic elements to correspond to the states of matter: earth (solid), water (liquid), air (gas), plus fire, which the Greeks saw as an element. Of course, since few objects are made of just one element, it was logical to assume they were compounds of two or more of the terrestrial elements. The Greeks spent a good deal of time figuring out the elements different objects contained by observing the qualities they exhibited. For example, wood is composed of earth (because it is solid), fire (because it burns), and air (because the ash left behind floats on top of water). Second, there was the observation that the stars, sun, planets, and moon seem to orbit the earth in perfect circles. Finally, all dropped objects seem to fall toward the center of the earth. These led to several important conclusions.

For one thing, the theory of four elements plus the perfect circular orbits of the stars and planets gave rise to the idea that the celestial bodies were made of a perfect element, ether. Ether was weightless or very light so the stars and planets could easily orbit the earth every day. It must also be perfect, incorruptible, and unrelated to the earthly elements since its motions are always in perfect circles, a motion rarely seen on earth.

Second, the motion of dropped objects toward the center of the earth (no matter where on earth they are dropped) and the apparent orbits of the heavenly bodies around the earth led to the geocentric theory, the idea that the earth is the center of the universe. Aristotle and most educated Greeks assumed the earth was round since one can see ships disappear over the horizon, the earth casts a round shadow on the moon during lunar eclipses, and the positions of the stars change as we move north or south.

Finally, there was Aristotle's law of motion. Aristotle saw that heavier objects (made of earth and water) have a tendency to fall or sink toward the center of the earth, while lighter objects (made of air and fire) rise or float. He called these tendencies of the elements to rise or fall natural motions and said that all elements have an inclination to rise or fall to their natural resting places in relation to one another. Aristotle called all other terrestrial motions forced or violent motions since they needed an outside force in constant contact with the object in order to take place. Thus the theory of four terrestrial (earthly) elements and the falling of those elements toward the center of the earth led to a law of motion which said everything must stay in contact with a prime mover in order to keep moving and could only be stopped by some other intervening object or force.

Toward a new universe: the downfall of Aristotle (1543-1687)

There were several factors that worked both to overthrow Aristotle's system and to preserve it. First of all, Aristotle's theories relied very little on experiment, which left them vulnerable to anyone who chose to perform such experiments. However, attacking one part of Aristotle's system involved attacking the whole thing, which made it a daunting task for even the greatest thinkers of the day. Secondly, the Church had grafted Aristotle's theories onto its theology, thus making any attack on Aristotle an attack on the tradition and the Church itself.

Finally, there were the Renaissance scholars who were uncovering other Greek authors who contradicted Aristotle. This was unsettling, since these scholars had a reverence for all ancient knowledge as being nearly infallible. However, finding contradicting authorities forced the Renaissance scholars to try to figure out which ones were right. When their findings showed that neither theory was right, they had to think for themselves and find a new theory that worked. This encouraged skepticism, freethinking, and experimentation, all of which are essential parts of modern science.

Pattern of development

The combination of these factors generated a cycle that undermined Aristotle, but also slowed down the creation of a new set of theories. New observations would be made that seemed to contradict Aristotle's theories. This would lead to new explanations, but always framed in the context of the old beliefs, thus patching up the Aristotelian system. However, more observations would take place, leading to more patching of the old system, and so on. The first person who started this slow process of dismantling Aristotle's cosmology was Copernicus. His findings would reinforce the process of finding new explanations, which would lead to the work of Kepler and Galileo. The work of these three men would lead to many new questions and theories about the universe until Isaac Newton would take the new data and synthesize it into a new set of theories that more accurately explained the universe.

Nicolaus Copernicus

was a Polish scholar working at the University of Padua in northern Italy. The problem he wrestled with was the paths of planetary orbits. Through the centuries close observations had shown that the heavens do not always appear to move in perfect, uninterrupted circles. Rather, they sometimes seem to move backwards in what are known as retrogradations. (This, in fact, occurs when Earth passes another planet in its orbit, thus making it appear to go backwards.) In order to account for these irregularities, astronomers did not do away with Aristotle's theory of perfectly circular orbits around the earth. Instead, they expanded upon it, adding smaller circular orbits (epicycles) that spun off the main orbits. These more or less accounted for the retrogradations seen in orbits. Each time a new irregularity was observed, a new epicycle was added. By the 1500's, the model of the universe had some 80 epicycles attached to ten crystalline spheres (one for the moon, sun, each of the five known planets, the totality of the stars, a sphere to move the other spheres, and heaven). The second century Greek astronomer, Ptolemy was the main authority who put order to and passed this cumbersome system of epicycles to posterity.

Copernicus' solution was basically geometric. By placing the sun at the center of the universe and having the earth orbit it, he reduced the unwieldy number of epicycles from 80 to 34. His book, Concerning the Revolutions of the Celestial Worlds, published in 1543, laid the foundations for a revolution in how Europeans would view the world and its place in the universe. However, Copernicus' intention was not to create a radically new theory, but to get back to even older ideas by such Greeks as Plato and Pythagoras who believed in a heliocentric (sun centered) universe. Once again, ancient authorities were set against one another, leaving it for others to develop their own theories.

It took some 150 years after Copernicus' death in 1543 to achieve a new model of the universe that worked. The first step was compiling more data that tarnished the perfection of the Ptolemaic universe and forced men to re-evaluate their beliefs.

Johannes Kepler

At this time, Tycho Brahe, using only the naked eye, tracked the entire orbits of various stars and planets. Previously, astronomers would only track part of an orbit at a time and assume that orbit was in a perfect circle. Brahe kept extensive records of his observations, but did not really know what to do with them. That task was left to his successor, Johannes Kepler.

Kepler was a brilliant mathematician who had a mystical vision of the mathematical perfection of the universe that owed a great deal to the ancient Greek mathematician Pythagoras. Despite these preoccupations, Kepler was open minded enough to realize that Brahe's data showed the planetary orbits were not circular. Finally, his calculations showed that those orbits were elliptical.

Galileo

As important as Kepler's conclusions was his method of arriving at it. He was the first to successfully use math to define the workings of the cosmos. Although such a conclusion as elliptical orbits inevitably met with fierce opposition, the combination of Brahe's observations and Kepler's math helped break the perfection of the Aristotelian universe. However, it was the work of an Italian astronomer, Galileo Galilei (1564-1642), armed with a new invention, the telescope, which would further shatter the old theory and lead the way to a new one.

In the year 1608, several Flemish gentlemen arrived in Venice carrying a startling new invention: the telescope. Upon hearing of this, Galileo, who was then working in Venice, quickly figured out its principles and built one himself, increasing its magnification from three times to ten. He got the Venetian senate excited about the telescope as an early warning device that could spot enemy ships twenty miles away and make them appear as if they were only two miles away. Galileo's curiosity was a bit more far ranging than spotting enemy ships, and eventually he turned his gaze toward the skies. That was when trouble began.

The impact of that first telescope can better be appreciated by imagining how our views of the universe might change if our technology increased our view of the universe by a factor of ten times. Galileo's findings were probably more disturbing. He saw the sun's perfection marred by sunspots and the moon's perfection marred by craters. He also saw four moons orbiting Jupiter. In his book, The Starry Messenger (1611), he reported these disturbing findings and spread the news across Europe. Most people could not understand Kepler's math, but anyone could look through a telescope and see for himself the moon's craters and Jupiter's moons.

The Church tried to preserve the Aristotelian and Ptolemaic view of the universe by clamping down on Galileo and his book and made him promise not to preach his views. However, in 1632, Galileo published his next book, Dialogue on the Great World Systems, which technically did not preach the Copernican theory (which Galileo believed in), but was only a dialogue presenting both views "equally". Galileo got his point across by having the advocate of the Church and Aristotelian view named Simplicius (Simpleton). He was quickly faced with the Inquisition and the threat of torture. Being an old man of 70, he recanted his views. However, it was too late. Word was out, and the heliocentric heresy was gaining new followers daily.

Galileo's work was the first comprehensive attack on the Aristotelian/Ptolemaic cosmic model. He treated celestial objects as being subject to the same laws as terrestrial objects. However, Galileo was still enthralled with perfect circular motion and, as a result, did not come up with the synthesis of all these new bits of information into a new comprehensive model of the universe. This was left to the last, and probably greatest, giant of the age, Isaac Newton.

Meanwhile, two celestial phenomena added further doubts about the Aristotelan system. First, a bright new star (probably a supernova explosion) suddenly appeared in 1572. Within a year, it was gone from the sky, leaving in its wake doubts about the changeless perfection of the stars. Five years later, a new comet cut across the skies and through the crystalline spheres that were supposed to hold the stars and planets in their orbits. Of course, the question was raised: did such perfect spheres even exist, and, if they did, how could a comet cross through them?

One needs to understand the new problems that the discoveries of the 1500's and early 1600's presented for seventeenth century scientists. Galileo's work had done more to destroy the Aristotelian system than create a new working one. As a result, there was great confusion among scholars as to what the structure of the universe really was. There were three major problems confronting them. One problem bothering seventeenth century scientists concerned the nature of motion. Aristotle's law of inertia said basically two things:

1. An object is naturally at rest unless moving toward its natural resting place. It takes forced or violent action to move that object, and that force must be in constant contact for the object to keep moving.

2. The object will keep moving until something else intervenes to stop it.

The main problem with Aristotle's law of inertia was the assumption that the moving object had to be in constant contact with the moving force. For example, the question was raised of how could an arrow keep flying once removed from the force driving it. This was explained by saying the air being displaced by the arrow went around behind it and pushed it along. This seemed unlikely, since the same air driving the arrow also would also be slowing it down.

This concept of a prime mover had bothered Renaissance scholars, who then came up with the new theory of Impetus. According to this, moving objects were carried forward by some vague force within the object or imparted to it like the heat in a red-hot piece of iron. The theory of impetus allowed people to discuss motion after contact with a mover was broken. There was just one problem with this theory: it was wrong. Nevertheless, it was an important theory because it challenged Aristotle's authority and opened the way to a new theory. The great French mathematician, Descartes, finally came up with the modern theory of inertia, which said a moving object will keep moving in a straight line until something interferes to stop it or slow it down.

The second problem bothering philosophers was what kept objects from flying out of their orbits and into space. Descartes, like Aristotle, did not believe in the existence of vacuums, since they would create no resistance to moving objects, thus allowing them to accelerate to infinite speed, which, of course, is both impossible and absurd. Space, according the Descartes, was filled with ether and cosmic whirlpools that kept the planets in orbit. Not everyone discounted the existence of vacuums, especially since the experiments of Galileo's student, Toricelli, with barometric pressure proved that vacuums can and do exist. Once again this raised the problem of what keeps the planets and stars in orbit if ether did not

The Englishman, William Gilbert offered a solution in 1600, suggesting that magnetism was the answer. He saw the earth as a giant magnet, keeping both terrestrial and celestial objects from flying off into space. Although his theory was basically wrong, it did open people's minds to the idea of objects exerting a pull on one another. As a result, in 1643, the Frenchman, Roberval, suggested a theory of universal gravitation, the tendency of all matter to have an attraction for all other matter. However, he did not have the math to prove the theory.

Even if Roberval's theory of gravity were right, it raised a third problem: what keeps the moon and other celestial bodies from falling to earth? For Roberval, it was the resistance of ether in space. In 1665, Alphonse Borelli suggested centrifugal force. A mathematician named Huygens figured out the formula for centrifugal force, but he also believed in circular motion. And there was still the problem of what kept the sun, moon, planets, and stars in their orbits. That was where Isaac Newton came in.

The story of Newton being hit on the head by an apple may very well be true. However, the significance of this popular tale is usually lost. People had seen apples fall out of trees for thousands of years, but Newton realized, in a way no one else had realized, that the same force pulling the apples to earth was keeping the moon in its orbit. Of course, Roberval had suggested this before, but Newton proved it mathematically. In order to do this, he had to invent a whole new branch of math, calculus, for figuring out rates of motion and change. The genius of Newton in physics, as well as William Harvey in medicine and Mendeleev in chemistry, was not so much in his new discoveries, as in his ability to take the isolated bits and pieces of the puzzle collected by his predecessors and fit them together. In retrospect, his synthesis seems so simple, but it took tremendous imagination and creativity to break the bonds of the old way of thinking and see a radically different picture.

The implications of Newton's theory of gravity can easily escape us, since we now take it for granted that physical laws apply the same throughout the universe. To the mentality of the 1600’s, which saw a clear distinction between the laws governing the terrestrial and celestial elements, it was a staggering revelation. His three laws of motion were simple, could be applied everywhere, and could be used with calculus to solve any problems of motion that came up.

The universe that emerged was radically different from that of Aristotle. Thanks to Newton, it was within our grasp to understand, predict, and increasingly manipulate the laws of the universe in ways no one had been able to do before. Newton's work also completed the fusion of math promoted by Renaissance humanists, Aristotelian logic pushed by medieval university professors, and experiment to test a hypothesis pioneered by such men as Leonardo da Vinci and Galileo into what we call the scientific method. This fusion had gradually been taking place since the Renaissance, but the invention of calculus made math a much more dynamic tool in predicting and manipulating the laws of nature.

The printing of Newton's book, Principia Mathematica, in 1687 is often seen as the start of the Enlightenment (1687-1789). It was a significant turning point in history, for, armed with the tools of Newton's laws and calculus, scientists had an unprecedented faith in their ability to understand, predict, and manipulate the laws of nature for their own purposes. This sense of power popularized science for other intellectuals and rulers in Europe, turning it into virtual religion for some in the Enlightenment. Even the geometrically trimmed shrubbery of Versailles offers testimony to that faith in our power over nature. Not until this century has that faith been seriously undermined or put into a more realistic perspective